Digital Debunking: Can You Actually Shatter Glass with Your Voice?
Setting the Stage
An opera singer hits a high note, rattling the audience’s ear drums and exploding a wine glass in the drawing room. You may have seen this in the movies, but is this really possible with sound alone? Is an acoustic assault from the human voice powerful enough to shatter glass?
If you asked someone off the street to try this experiment, they’d likely attempt to do two things: sing as loud as they possibly can and sing in the highest possible pitch. The result? All the dogs in the neighborhood might start barking, but the glass would very likely remain intact. A person could scream himself or herself blue in the face, but at the wrong pitch most of the forces from his or her voice would be reflected, leaving the glass unharmed.
Requiring both power and precision, there is a secret to breaking glass with your voice alone; a magic tone unique to every object. An object free to vibrate tends to do so at a specific rate, called its natural or resonant frequency. This frequency depends on the size, shape, and composition of the object. An object will vibrate strongly with virtually no dampening when it is subjected to vibrations at its resonant frequency. Conversely, it reflects much of the force outside this natural resonance range. The pure sound given off when you strike a crystal glass is the glass’ resonant frequency, and in theory, if a singer matches pitch with enough volume, the forces will be powerful and concentrated enough to shatter the glass.
Behind the Scenes
In order to prove this theory, we set up a simulation to see if a crystal wine glass would break within the possible volume and range of the human voice. A trained opera singer can sustain a note at or slightly above 100 decibels (dB), nearly the volume of a jackhammer. We also needed to determine if the resonant frequency could be reached within a singer’s potential pitch range. Average speech is typically between a frequency of 100 to 220 hertz (Hz) and a professional soprano's frequency ranges anywhere from 250 to 1,500 Hz.
The most important determination is the exact resonant frequency of the glass itself. If you stimulate the wine glass with sound at that frequency, the vibrations in the glass will be much more intense than at any other frequency. If they are intense enough, the glass will break.
One of the secrets of breaking the glass is the resonant frequency changes slightly, as the glass vibrates with a larger displacement. When you tap the glass to hear the resonant frequency, that is slightly higher (by a few Hz) than the frequency you’ll need to break the glass.
Preparing for Showtime: Setting up the Simulation
This classic demonstration of resonance uses intense sound waves whose frequency is tuned to match the natural frequency of a wine glass. The glass has a high lead content, which produces the high-quality factor, Q, required for this demonstration. The “quality” of the glass can be heard by noting how long it rings after tapping. The natural frequency of the wine glass to be used is carefully measured before the demonstration to be within ~ 0.1 Hz. When driven by an amplifier and speaker, the standing waves excited along the circumference of the wine glass take about a second to build to maximum amplitude and break the wine glass. It should be emphasized frequency matching is crucial, and no amplitude of a poorly matched audio signal will be enough to break the wine glass.
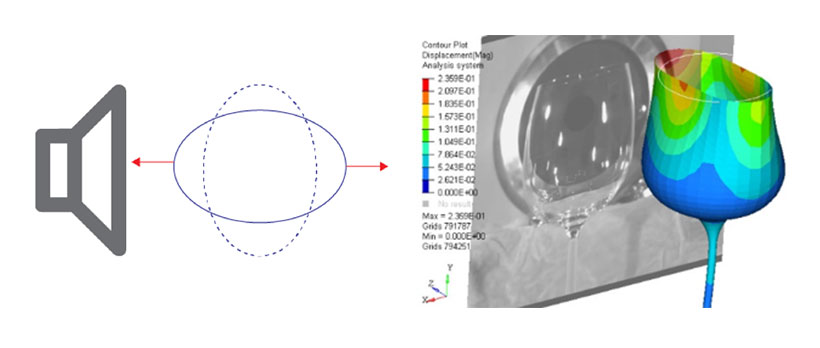
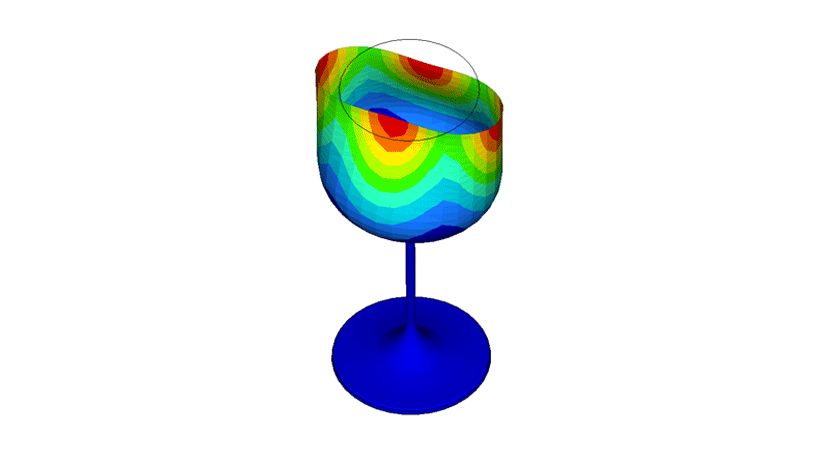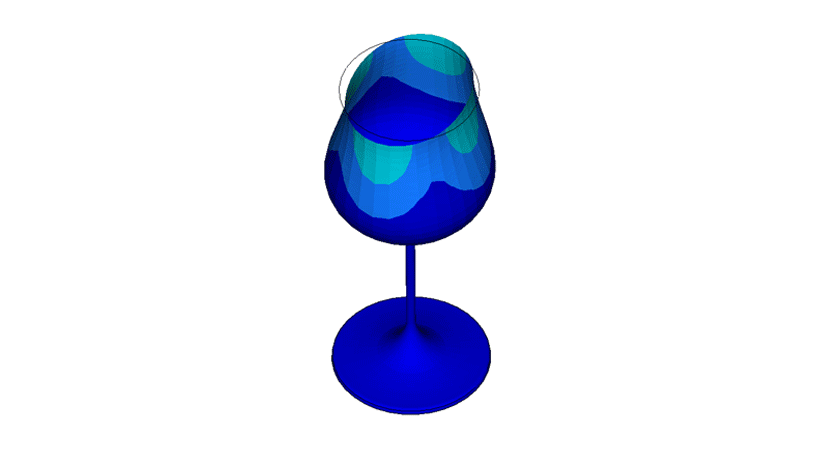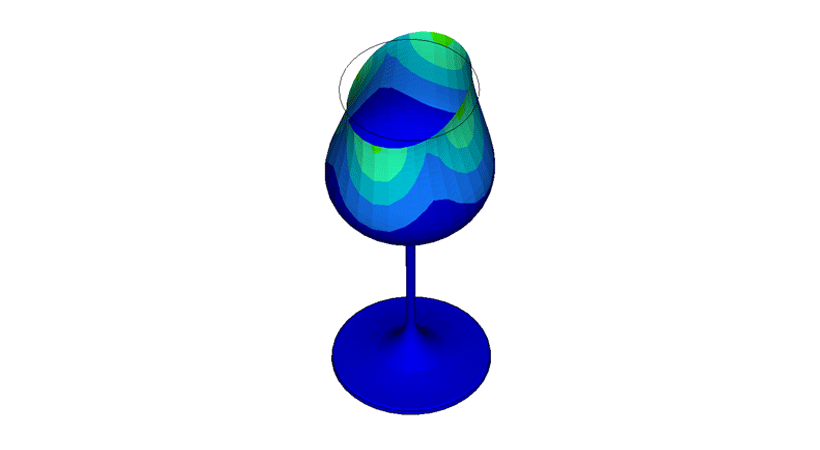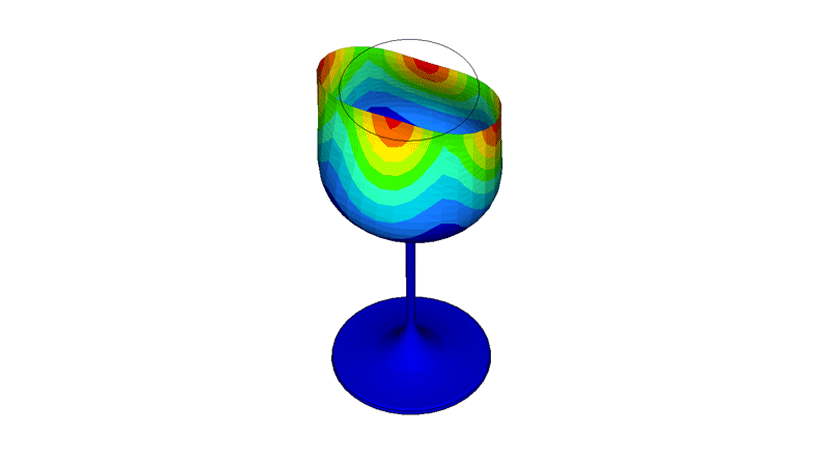
To simulate this phenomenon, initially we needed to create a finite model of a wine glass and obtain the resonance frequency and its mode shapes. Modes are the various ways in which energy can be dynamically stored in a system, oscillation between kinetic and potential energies. In the simulation world, we are able to see these mode shapes at each resonance frequency of the structure and here we have snapshot for these mode shapes below from the Altair OptiStructTM normal mode analysis.
A resonance frequency of 392.2 Hz was determined to have the mode shape that could sufficiently distort the shape of the wine glass bowl, as well as the stem and the foot of the glass. This frequency is well within the possible range of the human voice. We then built an acoustic domain around the glass and excited it with this high loading.
The Main Event: Running the Simulation
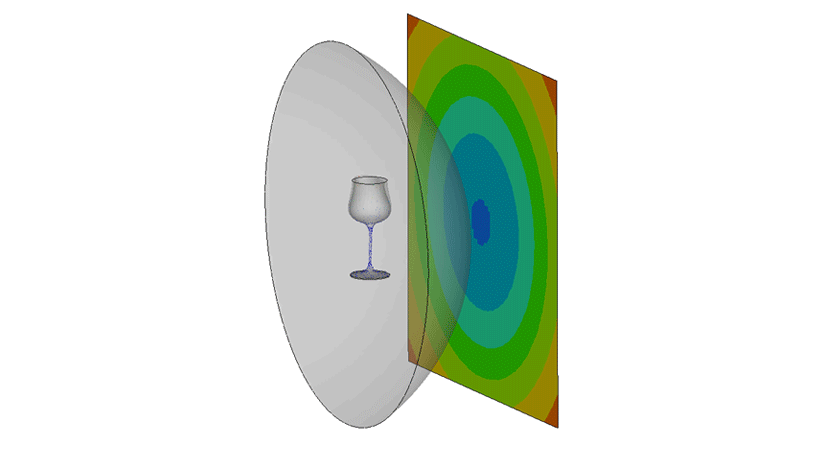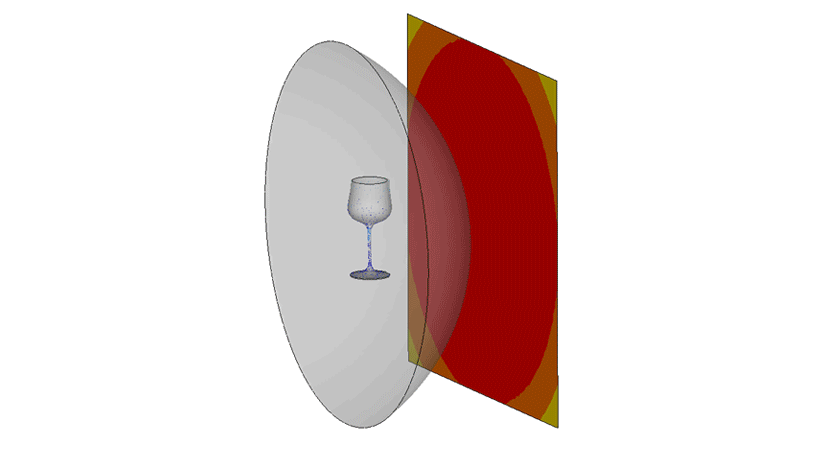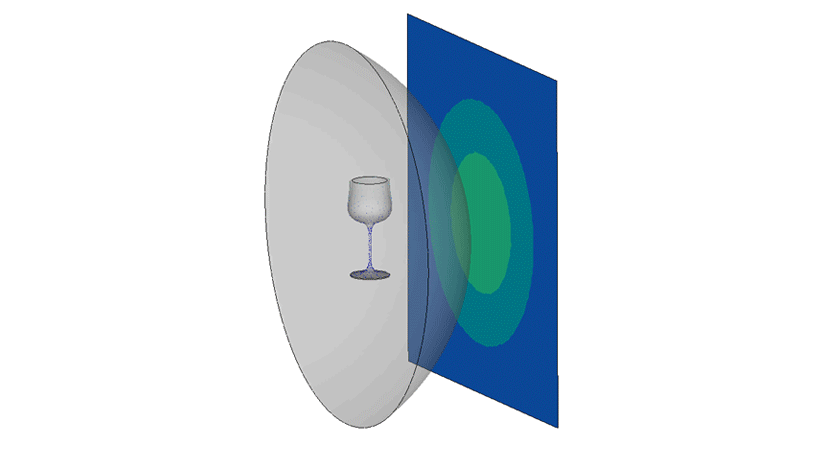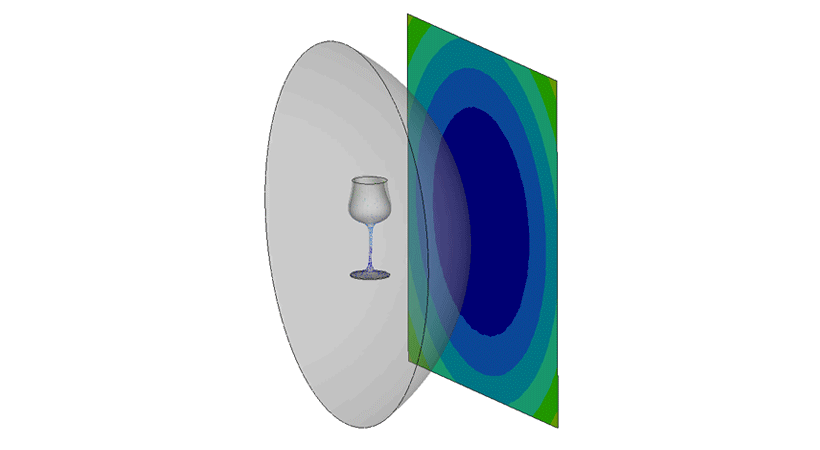
Generally, acoustic internal radiation problems are solved based on inviscid flow with linear pressure density relation. Infinite elements are typically used to simulate external radiation problems. Acoustic modeling, in finite and semi-infinite domains, are essential in the prediction of quantities, such as external and radiated noise in vibro-acoustic problems. Infinite elements are a popular way of modeling these domains. Acoustic infinite elements are used here to simulate the external sound pressure on the receiver.
This finite element model has a sound pressure source at the center of the fluid sphere. Inside the sphere, the wine glass vibrates from excitation received from the sound source. The infinite elements are the skin of the sphere whose element normals are pointing towards the receiver. This is modeled here to monitor the sound pressure in the range of 110 dB to 140 dB, in the upper limits of the human voice’s sustainable volume.
In the acoustic results, we observed the wine glass is vibrating at 392.2 Hz and the wine bowl circumference is generating very high displacements, and negatable at the stem and foot. While on the receiver plate, we observed a very high sound pressure, above 140 dB. The maximum displacement observed was between 120-140 dB.
The Crescendo: Did the Glass Break?
When we turned on the failure predictions in the finite element solver with the displacement values at 120-140 dB, we observed the glass breaking between a range of 1k-10k sinusoidal curve (0.00243 sec/cycle). This equates to less than 20 total seconds, within the range a singer could sustain a note. In the simulation images below, you can see the crack initialized from the top the bowl at the circumference.
The simulation supported our initial hypothesis. A note sustained for 20 seconds at the resonant frequency of the glass created enough displacement for the bowl to break. Interestingly, the focus section breaks all at once as the glass shatters. Glass is a great test for this resonance phenomenon, since it is so brittle. There are not many energy absorbing mechanisms in glass, so all the energy goes into extending the length of cracks, which happens very quickly and shatters the wine glass in an abrupt and dramatic fashion.

In this simulation, we see a powerful representation of the unseen forces around us and how the propagation of mechanical vibrations can physically impact objects. That’s music to our ears.
An opera singer hits a high note, rattling the audience’s ear drums and exploding a wine glass in the drawing room. You may have seen this in the movies, but is this really possible with sound alone? Is an acoustic assault from the human voice powerful enough to shatter glass?
If you asked someone off the street to try this experiment, they’d likely attempt to do two things: sing as loud as they possibly can and sing in the highest possible pitch. The result? All the dogs in the neighborhood might start barking, but the glass would very likely remain intact. A person could scream himself or herself blue in the face, but at the wrong pitch most of the forces from his or her voice would be reflected, leaving the glass unharmed.
Requiring both power and precision, there is a secret to breaking glass with your voice alone; a magic tone unique to every object. An object free to vibrate tends to do so at a specific rate, called its natural or resonant frequency. This frequency depends on the size, shape, and composition of the object. An object will vibrate strongly with virtually no dampening when it is subjected to vibrations at its resonant frequency. Conversely, it reflects much of the force outside this natural resonance range. The pure sound given off when you strike a crystal glass is the glass’ resonant frequency, and in theory, if a singer matches pitch with enough volume, the forces will be powerful and concentrated enough to shatter the glass.
Behind the Scenes
In order to prove this theory, we set up a simulation to see if a crystal wine glass would break within the possible volume and range of the human voice. A trained opera singer can sustain a note at or slightly above 100 decibels (dB), nearly the volume of a jackhammer. We also needed to determine if the resonant frequency could be reached within a singer’s potential pitch range. Average speech is typically between a frequency of 100 to 220 hertz (Hz) and a professional soprano's frequency ranges anywhere from 250 to 1,500 Hz.
The most important determination is the exact resonant frequency of the glass itself. If you stimulate the wine glass with sound at that frequency, the vibrations in the glass will be much more intense than at any other frequency. If they are intense enough, the glass will break.
One of the secrets of breaking the glass is the resonant frequency changes slightly, as the glass vibrates with a larger displacement. When you tap the glass to hear the resonant frequency, that is slightly higher (by a few Hz) than the frequency you’ll need to break the glass.
Preparing for Showtime: Setting up the Simulation
This classic demonstration of resonance uses intense sound waves whose frequency is tuned to match the natural frequency of a wine glass. The glass has a high lead content, which produces the high-quality factor, Q, required for this demonstration. The “quality” of the glass can be heard by noting how long it rings after tapping. The natural frequency of the wine glass to be used is carefully measured before the demonstration to be within ~ 0.1 Hz. When driven by an amplifier and speaker, the standing waves excited along the circumference of the wine glass take about a second to build to maximum amplitude and break the wine glass. It should be emphasized frequency matching is crucial, and no amplitude of a poorly matched audio signal will be enough to break the wine glass.
To simulate this phenomenon, initially we needed to create a finite model of a wine glass and obtain the resonance frequency and its mode shapes. Modes are the various ways in which energy can be dynamically stored in a system, oscillation between kinetic and potential energies. In the simulation world, we are able to see these mode shapes at each resonance frequency of the structure and here we have snapshot for these mode shapes below from the Altair OptiStructTM normal mode analysis.
A resonance frequency of 392.2 Hz was determined to have the mode shape that could sufficiently distort the shape of the wine glass bowl, as well as the stem and the foot of the glass. This frequency is well within the possible range of the human voice. We then built an acoustic domain around the glass and excited it with this high loading.
The Main Event: Running the Simulation
Generally, acoustic internal radiation problems are solved based on inviscid flow with linear pressure density relation. Infinite elements are typically used to simulate external radiation problems. Acoustic modeling, in finite and semi-infinite domains, are essential in the prediction of quantities, such as external and radiated noise in vibro-acoustic problems. Infinite elements are a popular way of modeling these domains. Acoustic infinite elements are used here to simulate the external sound pressure on the receiver.
This finite element model has a sound pressure source at the center of the fluid sphere. Inside the sphere, the wine glass vibrates from excitation received from the sound source. The infinite elements are the skin of the sphere whose element normals are pointing towards the receiver. This is modeled here to monitor the sound pressure in the range of 110 dB to 140 dB, in the upper limits of the human voice’s sustainable volume.
In the acoustic results, we observed the wine glass is vibrating at 392.2 Hz and the wine bowl circumference is generating very high displacements, and negatable at the stem and foot. While on the receiver plate, we observed a very high sound pressure, above 140 dB. The maximum displacement observed was between 120-140 dB.
The Crescendo: Did the Glass Break?
When we turned on the failure predictions in the finite element solver with the displacement values at 120-140 dB, we observed the glass breaking between a range of 1k-10k sinusoidal curve (0.00243 sec/cycle). This equates to less than 20 total seconds, within the range a singer could sustain a note. In the simulation images below, you can see the crack initialized from the top the bowl at the circumference.
The simulation supported our initial hypothesis. A note sustained for 20 seconds at the resonant frequency of the glass created enough displacement for the bowl to break. Interestingly, the focus section breaks all at once as the glass shatters. Glass is a great test for this resonance phenomenon, since it is so brittle. There are not many energy absorbing mechanisms in glass, so all the energy goes into extending the length of cracks, which happens very quickly and shatters the wine glass in an abrupt and dramatic fashion.

In this simulation, we see a powerful representation of the unseen forces around us and how the propagation of mechanical vibrations can physically impact objects. That’s music to our ears.