A modal analysis is used to find the natural frequencies along with the corresponding shape of the structure at each frequency.  This information is important for understanding the dynamic behavior of a structure. One primary objective of the modal analysis is to make sure the structure is not operating (vibrating) at a frequency close any of its natural frequencies.

Finding modes with traditional FEA

In traditional FEA, finding modes can be problematic. For a given structure, there is an infinite number of vibration modes, however FEA modes are limited by the number of degrees of freedom available in the finite element model. The lowest modes with simple shapes are usually easy to find, but it becomes increasing more difficult to capture the modes with higher frequencies and more complex mode shapes.
There are many “rules of thumb” of how many elements, etc are required. Complicating this further, many modal eigen-solvers are sensitive to the kind, size and shape of the elements used. In most cases, remeshing is required to understand convergence, but this is problematic in itself for complex parts and large assemblies.
Modes are sensitive to the mass and stiffness available in the model. Simplification of the geometry is common to make meshing easier, but this can lead to errors if critical mass or stiffness features are left out.
With traditional FEA, the user is forced to understand the strengths of various solver methods (Lanczos, Subspace, Householder, etc) and solvers (Sparce, PCG, etc.). In addition, to capture high frequencies, many parameters (iteration limits, convergence tolerances, lumped or consistent mass matrices, master DOF, and more) often need to be set and “tweaked” in order to get a solution.

There is a better way

Altair SimSolid makes the process of finding modes much easier. Since it works with the full CAD geometry, the true mass and stiffness is better represented. Adaptive solution refinement allows a single model to capture low to high frequency modes even for large assemblies. And, the completeness of Altair SimSolid’s high order approximation functions used to represent modal shapes makes it less likely for it to miss any modes.
With Altair SimSolid there are no solver types or options to set. Global and local solution refinement makes it easy to examine modal convergence, even for large models. No meshing or remeshing is required. Best of all, solution times are typically fast – seconds to minutes, even when asking for large number of modes. This makes it easy to create and evaluate a structure’s modal content.

High frequency example

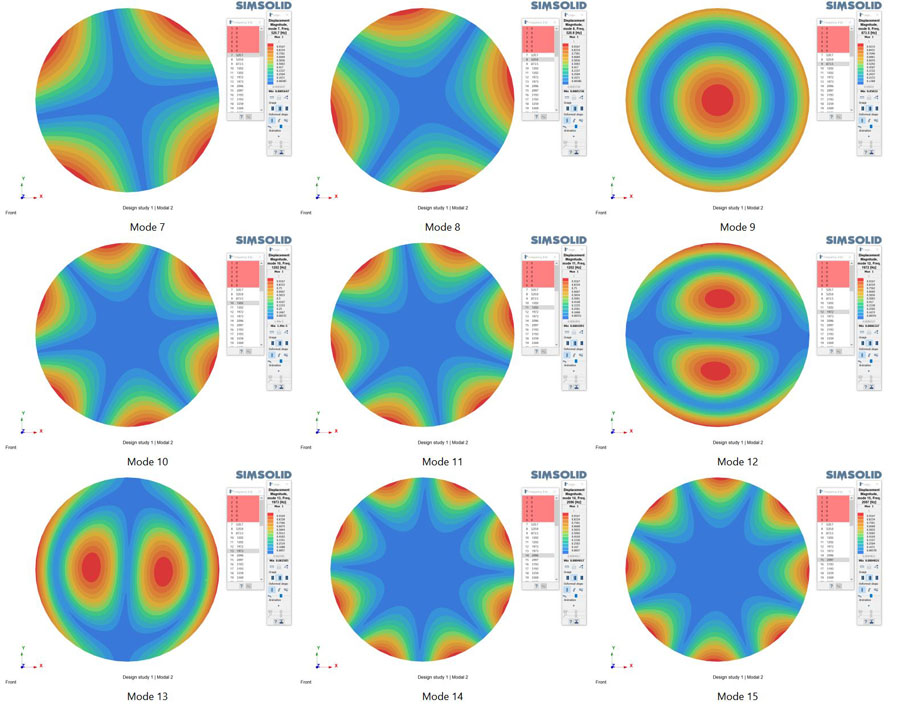
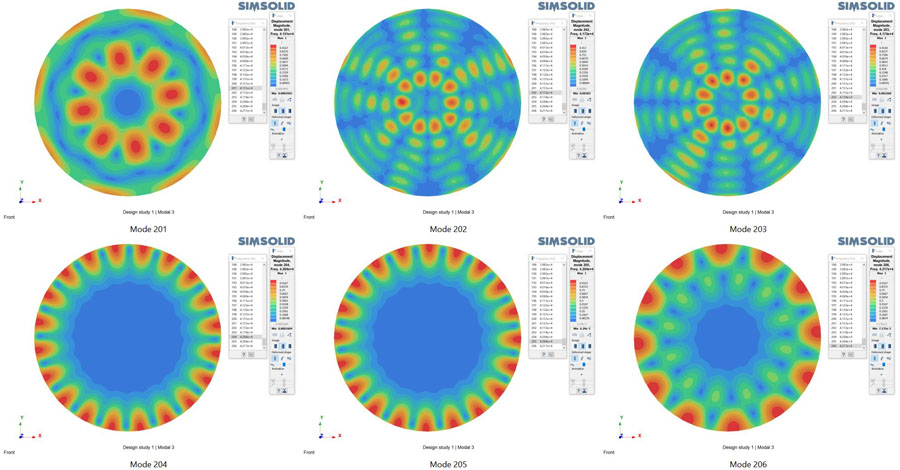
Here is an example of circular steel plate. Three modal analyses are performed on the unconstrained model that capture respectively the first 5, 50 and 200 flexible modes. All runs are performed on a standard Intel I7 desktop computer with standard solution settings. Solution times for all analyses are relatively fast – even the largest ran in under 4 minutes. As one can see, Altair SimSolid is able to capture the details of high frequency modes with high resolution.

Table of solution times

 

First 9 flexible modes

 

High frequency modes - modes 201 through 206

 

 

Modes for large assembly

Finally, here is a video of modes being calculated on a more realistic model. This is a truss structure with 500+ parts with a variety of shapes and full CAD geometric detail.
https://www.youtube.com/watch?v=ZFDbL3YmeRc