Neuber Correction: Correcting Elastic Stresses for Plasticity
The world is nonlinear, we all know that. The need to accurately represent complex real-world phenomenon has increased given the demand on design and the increased competition in developing these designs. However, running simulations to capture these complex nonlinear behaviors can be very expensive and take several hours to run. This burden is magnified if the requirement is to optimize the design, as now, the solution time could potentially run in to multiple days! This is the motivation to come up with efficient and quicker solutions without compromising on accuracy. The Neuber correction is one such solution that allows the evaluation of plasticity in a structure via a linear analysis and therefore avoids having to run a full-fledged nonlinear analysis. This is particularly valuable in the design development phase when multiple such studies are needed to be run; the Neuber correction approach saves a significant amount of time and improves the overall workflow.
The Neuber method corrects elastic results to capture any local plasticity. It is used to convert elastic stress/strain into real stress/strain when plastic deformation occurs. To apply Neuber’s rule, compute stress (KtS) at a notch with elastic assumptions and when the stress exceeds the strength of the material, the real stress will be somewhere on the materials stress-strain curve at a point σ.
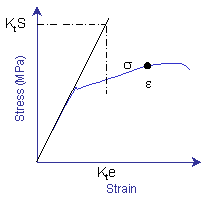
Neuber's rule states that the stress-strain product of the elastic solution is equal to the stress-strain product of the real elastic-plastic solution. Mathematically, this is expressed as:
KtS⋅Kte=σ⋅ε
This method is commonly used to predict the local cyclic stress/strain, when components are subjected to fatigue loading, making it easy to extend and capture local plasticity for static load cases to save computational time and enable optimization. A simple example is shown below. The model is part of an aircraft landing gear.
Neuber stresses are evaluated for one of the durability load cases which represent the aircraft landing with maximum pay load condition. The load case is represented by fully constraining the model and a force load of 1.5E6 N applied at the center of the boss in the vertical direction.
The results in picture 3 show how the stresses in the lug compared for the three different analysis approaches. The peak Neuber stress obtained by running linear analysis with Neuber correction is 340 MPa which matches very well with peak real stress obtained by running full-fledged nonlinear analysis. On the other hand, the elastic stresses are quite off from the real stress. Utilizing linear analysis to capture Neuber stress is three times faster than running a full-fledged nonlinear analysis for this model.
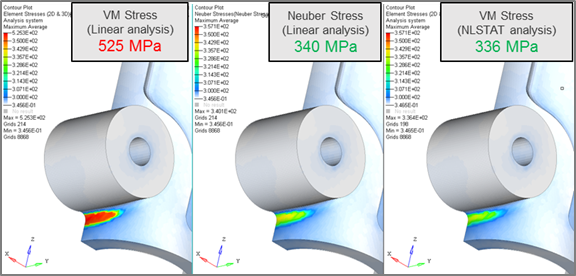
Picture 3: Stress Results (Linear, Neuber, Nonlinear)
Since running linear analysis to capture real stresses is much faster compared to running a full-fledged nonlinear analysis, it also enables optimization. The model was setup to run shape optimization to locally target the stresses which are beyond yield. The optimization formulation was to limit the Neuber stresses in the component to be below yield with minimum amount of mass added.
The optimization converged with a feasible design. Neuber stresses of the optimized design are now below yield and was achieved by increasing the mass by 1%. Below is a picture of the shape change that helped achieve the target to keep the Neuber stresses in the model below yield.
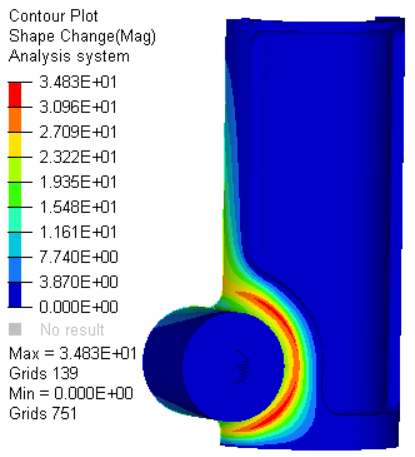
Picture 4: Shape Change from Optimization
To summarize, Neuber stresses obtained by running linear analysis and Neuber correction can be used to evaluate local plasticity accurately. This method is also computationally inexpensive and helps to enable optimization. Altair® OptiStruct® has the capability to output the Neuber stresses without running a full-fledged nonlinear analysis; these stresses can also be output when nonlinear analysis with sliding contact is performed without explicitly evaluating plasticity. Neuber stress/strain can also be used as responses (constraints/objective) to perform optimization.
Interested in learning more about the capabilities of OptiStruct? Check out our collection of on-demand webinars.





